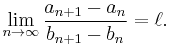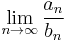Stolz–Cesàro theorem
In mathematics, the Stolz–Cesàro theorem, named after mathematicians Otto Stolz and Ernesto Cesàro, is a criterion for proving the convergence of a sequence.
Let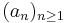 
and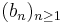 
be two sequences of real numbers. Assume that 
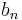is strictly increasing and unbounded and the following limit exists:
Then, the limit
also exists and it is equal to ℓ.
The Stolz–Cesàro theorem can be viewed as a generalization of the Cesàro mean, but also as a l'Hôpital's rule for sequences. The ∞/∞ case is stated and proved on pages 173--175 of Stolz's 1885 book S and also on page 54 of Cesàro's 1888 article C. It appears as Problem 70 in PS.
References
- Marian Mureşan: A Concrete Approach to Classical Analysis. Springer 2008, ISBN 9780387789323, p. 85 (restricted online copy at Google Books)
- Stolz, O. Vorlesungen über allgemeine Arithmetik: nach den Neueren Ansichten, Teubners, Leipzig, 1885, pp. 173--175.
- Cesaro, E. , Sur la convergence des séries, Nouvelles annales de mathématiques Series 3, 7 (1888), 49--59.
- Pólya, G. and Szegö, G. Aufgaben und Lehrsätze aus der Analysis, v. 1, Berlin, J. Springer 1925.
External links
This article incorporates material from Stolz-Cesaro theorem on PlanetMath, which is licensed under the Creative Commons Attribution/Share-Alike License.